Open-Source GeoFNO Implementation for Irregular Geometries in PDE Solvers
Introduction
Partial differential equations (PDEs) are essential for simulating physical phenomena across fields such as engineering, environmental science, and healthcare. They enable us to model complex processes like fluid flow in engines, pollutant dispersion in the air, and blood circulation in arteries. However, traditional PDE solvers are limited in handling irregular geometries, which constrains their effectiveness in real-world applications. This project aims to overcome this limitation by implementing Geo-FNO, a neural operator designed specifically for irregular geometries, within the Unified PDE Solver (UPS) framework.
By developing this open-source solution with OpenFOAM, we seek to provide accessible, accurate, and scalable simulation capabilities. For instance, this approach can improve the accuracy of simulations for designing safer bridges or predicting pollutant dispersion in urban areas. This advancement has the potential to improve safety in infrastructure, promote environmental sustainability, and enhance healthcare outcomes by enabling simulations that are closer to real-world scenarios.
Method
To address the need for irregular geometry handling, we integrated the Geo-FNO model—a specialized neural operator designed for irregular geometries—into a custom pipeline developed with OpenFOAM. My specific contributions to this project included conducting a comprehensive literature review to identify models capable of handling irregular geometries, setting up baselines for Navier-Stokes and Euler’s equations on airfoil and pipe flow problems, and implementing Geo-FNO for these PDEs. Other PDE implementations, such as elasticity and plasticity, were handled by collaborators, with guidance from our professor to address any issues encountered during the development.
Methodology Highlights:
- Leadership in Implementation: Spearheaded the development of a data generation pipeline and led the implementation of Geo-FNO for airfoil and pipe flow problems.
- Literature Review: Conducted an extensive review to identify foundational models for diverse PDE handling, specifically Geo-FNO for irregular geometries. Poseidon, another model reviewed, covers various PDEs but is restricted to regular geometries.
- Data Generation Pipeline: Designed an automated pipeline using Python and OpenFOAM scripts, capable of generating datasets with complex boundary conditions and geometries. This pipeline produced over 2,500 irregular pipe deformations and can be adapted for a wide range of PDEs.
- Geo-FNO Implementation: Implemented and tested Geo-FNO on the Navier-Stokes and Euler’s equations for airfoil and pipe flows to evaluate its performance on irregular domains. Collaborators focused on other PDEs like elasticity and plasticity. Comparisons were made with traditional interpolation methods to establish the advantages of using Geo-FNO.
- Experimentation with OpenFOAM: Leveraged OpenFOAM, an open-source software, to generate benchmark datasets, ensuring the pipeline is accessible for researchers and reproducible.
Visualization of Geo-FNO Architecture:
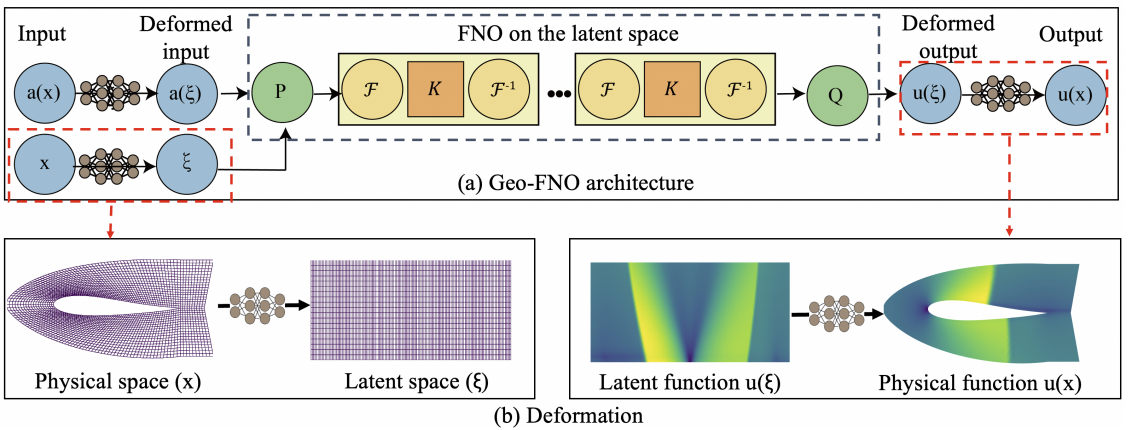
Figure 1: Geometry-aware FNO. The architecture deforms input functions from irregular physical space to a uniform latent space, applies FNO, and transforms back. (P) and (Q) are projection operators, while (\mathcal{F}) and (\mathcal{F}^{-1}) are Fourier transforms. (K) is a linear transform.
Results
The implementation of Geo-FNO on OpenFOAM has demonstrated promising results across multiple PDE types:
- Baseline Performance: Geo-FNO showed substantial improvements over traditional interpolation methods, achieving lower test losses on irregular pipe and elasticity datasets.
- Quantitative Outcomes:
- Pipe Flow with Hole Information: Train loss 0.06, test loss 0.09.
- Pipe Flow without Hole Information: Train loss 0.11, test loss 0.15.
- Elasticity Problem: Train loss 0.026, test loss 0.031.
- Airfoil Geometry: Train loss 0.31, test loss 0.13.
These results validate the efficacy of Geo-FNO on diverse, irregular geometries by achieving significantly lower errors than traditional methods, even on challenging datasets with highly variable geometries. This is a significant step forward, as it indicates that neural operator models can now be reliably used for complex real-world applications that were previously limited by traditional solvers.
- Open-Source and Reproducibility: The OpenFOAM-based pipeline ensures that our results can be reproduced and extended by other researchers, supporting the goal of an open-source solution for handling irregular geometries in PDE solvers.
Discussion and Future Directions
This project successfully implements Geo-FNO for handling irregular geometries, providing a new, accessible solution to complex PDEs. Our use of OpenFOAM ensures reproducibility and aligns with the open-source ethos, broadening access for researchers and practitioners.
Future Work:
- Integrating Geo-FNO with foundational models like Poseidon to enable comprehensive PDE solutions.
- Experimenting with larger datasets, such as the AirfoilMNIST dataset, to test out-of-distribution capabilities and scalability in more complex scenarios.
