Physics-Informed Diffusion Models for Physics-Based Data Generation

Introduction

Physics-Informed Diffusion Models (PIDMs) incorporate physical laws directly into the generative model’s training process, ensuring that generated data respects the governing equations associated with physical phenomena. Traditional diffusion models, though powerful, have lacked mechanisms to embed physical constraints into the data generation process. This project addresses this gap by integrating physics-based loss terms into the diffusion model training, enabling the generation of data that aligns with specific physical principles, such as partial differential equations (PDEs).

Social Impact: By ensuring that generated datasets follow physics principles, PIDMs can transform fields such as engineering simulations, environmental modeling, and material science. They provide researchers with cost-effective, reliable synthetic data that adheres to real-world physics, reducing reliance on computationally expensive simulations and promoting advancements in scientific understanding and innovation.

Methodology

Our approach involves augmenting standard denoising diffusion models with loss terms based on physical constraints, specifically PDE residuals, to enforce adherence to physics-based principles during data generation.

Data Collection and Preparation

I was responsible for generating the Darcy flow dataset using OpenFOAM, simulating steady-state fluid flow in porous media. This dataset was structured to facilitate training in the diffusion model. My teammate, in parallel, developed a dataset for topology optimization, broadening the applicability of the model to other physics-based domains.

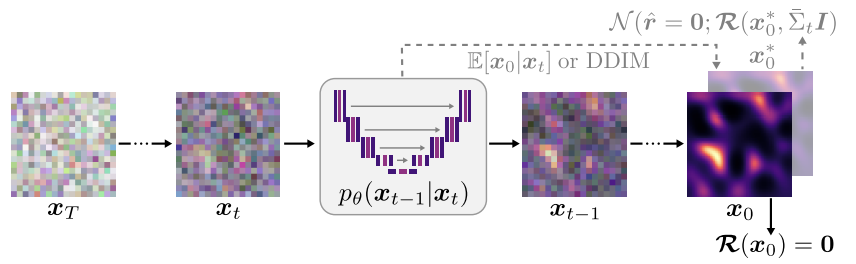
Figure 1: An approximation of the clean signal for residual evaluation can be obtained at any denoising timestep ( t ) using expected values or accelerated sampling methods.

Model Training

To integrate physics into the model, we collaboratively worked on incorporating a physics-based loss function that penalizes deviations from the governing equations. The training involved two main components:

• Physics-based Loss: This loss term was introduced to ensure that the generated samples adhere to physical constraints, such as boundary conditions and PDE residuals. The loss was specifically crafted to integrate finite differences to evaluate physics consistency over each generated sample.
• Data Likelihood: Standard diffusion training objectives were also retained to ensure that the generated samples maintain diversity and are statistically aligned with the training data.

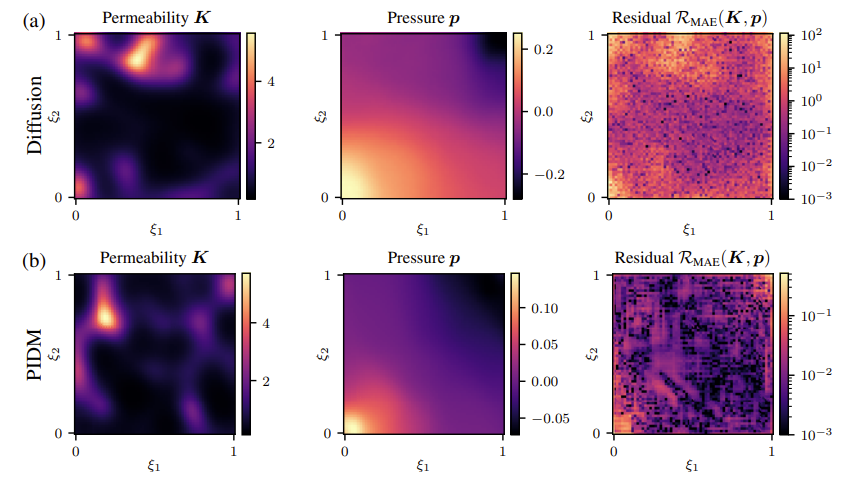
Figure 2: Comparison of residual error in permeability and pressure fields generated by (a) a standard diffusion model and (b) PIDM with mean estimation.

Results

The physics-informed diffusion model demonstrated significant improvements in generating physically consistent data:

• PDE Residuals Reduction: The physics-informed model reduced PDE residuals by over two orders of magnitude compared to traditional diffusion models, as evaluated on the Darcy flow dataset.
• Diversity in Physically Consistent Samples: The model successfully generated diverse datasets while adhering closely to physics constraints, showing robustness across both Darcy flow and topology optimization datasets.
• Training Efficiency: While incorporating physics-based losses introduced additional computation, the model maintained an efficient training process without significant slowdowns.

Discussion and Future Directions

Our results illustrate the feasibility of using diffusion models for physics-based data generation, overcoming limitations in previous data-driven models. This model can potentially serve as a resource for generating high-fidelity, physics-consistent datasets, which can support applications in scientific research and engineering design.

Future Work:

• Exploring other physical constraints and expanding the model’s applicability to more complex PDE systems.
• Integrating more sophisticated sampling techniques to further enhance the efficiency of the model while maintaining adherence to physics-based principles.